SQUARE ROOT OF IOTA

SQUARE ROOT OF COMPLEX NUMBERS

i, the square root of -1 the fundamental complex number. Working out the square-root of i;

ON MATLAB

Trying it on Matlab

Fig 1. Matlab 1

Fig 2. Matlab 2

Matlab gives very precise result both by 'power of 0.5' and 'sqrt function'.

USING CMATH

Using cmath module in Python;

Fig 3. cmath 1

Fig 4. cmath 2

cmath also gives wonderful results, however it is worth noting that the real and complex parts are different in the last 2 digits ( 0.70710678118654757 in the real part while 0.70710678118654746 in the complex part); which should not be so as they both represent the same number !

USING SCIPY

Using Scipy, scientific and numerical module in python

Fig 5. Using Scipy

Similar results to that of cmath.

SQUARING THE ROOT !

Squaring the square root often confirms to the accuracy and resolution of the software.

Fig 6. Squaring the root in Matlab

Fig 7. Squaring the root in cmath

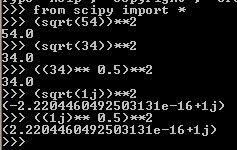
Fig 8. Squaring the root in scipy

SOME OBSERVATIONS

Matlab on squaring the root, gives precise results

cmath and scipy on squaring the root gives precise results for the complex part but odd results for the real part (2.2204460492503131e-16 for scipy and -2.2204460492503131e-16 for cmath).

Using (1j)**0.5 and sqrt(1j) in scipy yields different results in real parts (2.2204460492503131e-16 for (1j)**0.5 and -2.2204460492503131e-16 for sqrt(1j)).

For developing scipy there should be a sense of consistency with cmath and the resolution (digits in the answer) should be controlled at the discretion of the user( It really looks sleek in Matlab). Further it looks odd and conveys a sense of inconsistency if the complex part tallies completely with the expected result while the real part has an inconsistency.