SQUARE ROOT OF COMPLEX NUMBERSi, the square root of -1 the fundamental complex number. Working out the square-root of i;ON MATLABTrying it on Matlab
Fig 1. Matlab 1
Fig 2. Matlab 2
Matlab gives very precise result both by 'power of 0.5' and 'sqrt function'.
USING CMATH
Using cmath module in Python;
 Fig 3. cmath 1
Fig 3. cmath 1
Fig 4. cmath 2
cmath also gives wonderful results, however it is worth noting that the real and complex parts are different in the last 2 digits ( 0.70710678118654757 in the real part while 0.70710678118654746 in the complex part); which should not be so as they both represent the same number ! USING SCIPY
Using Scipy, scientific and numerical module in python
Fig 5. Using Scipy
Similar results to that of cmath.
SQUARING THE ROOT !
Squaring the square root often confirms to the accuracy and resolution of the software.
Fig 6. Squaring the root in Matlab
Fig 7. Squaring the root in cmath
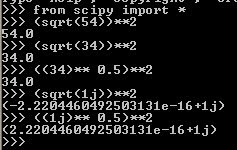
Fig 8. Squaring the root in scipy
SOME OBSERVATIONS
Matlab on squaring the root, gives precise results
cmath and scipy on squaring the root gives precise results for the complex part but odd results for the real part (2.2204460492503131e-16 for scipy and -2.2204460492503131e-16 for cmath).
Using (1j)**0.5 and sqrt(1j) in scipy yields different results in real parts (2.2204460492503131e-16 for (1j)**0.5 and -2.2204460492503131e-16 for sqrt(1j)).
For developing scipy there should be a sense of consistency with cmath and the resolution (digits in the answer) should be controlled at the discretion of the user( It really looks sleek in Matlab). Further it looks odd and conveys a sense of inconsistency if the complex part tallies completely with the expected result while the real part has an inconsistency.